登陆可实现PC、移动端同步进度.
ECharts 极坐标系
极坐标系是一个数学领域的概念，所以课程中我将会给大家阐述一下基本的概念，以防止有的同学不理解，而且，本小节涉及到图形公式较多，但是这些公式在网上都可以找到，所有请大家放心试用~
1. 简介
极坐标系，可以用于散点图和折线图。每个极坐标系拥有一个角度轴和一个半径轴。
慕课解释
极坐标系由极点、极轴、极径组成：
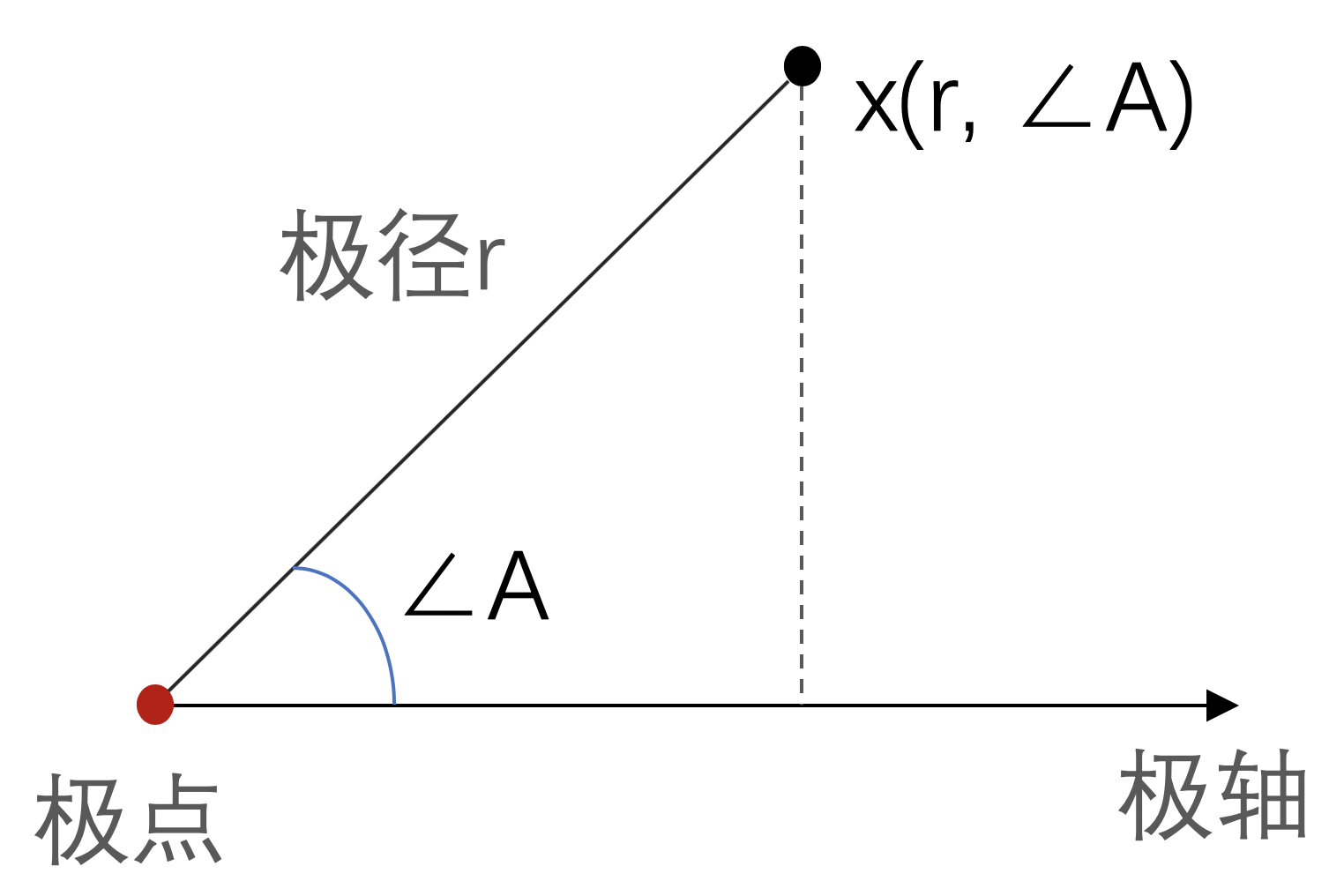
如图，在平面中任取一点 O 称为极点，由 O 出发任意取直线 ox 称为极轴，则平面上任意点 x 的坐标都可以使用点到极点的距离 r，以及点与极轴夹角的角度值 ∠a 表示，通常记录为 x(r, ∠a)。极坐标系支持折线图、散点图、柱状图类型。
2. 实例解说
2.1 基础示例
使用前，需要声明极坐标轴的容器、角度轴、径向轴，分别由下述属性定义：
polar：极坐标系容器配置，可定义坐标系位置、半径、提示效果等，对应直角坐标系中的grid项；angleAxis：角度轴配置，可定义角度轴边界、数据范围等，对应直角坐标系中的yAxis项；radiusAxis：径向轴配置，可定义径向轴的边界、数据范围等，对应直角坐标系中的xAxis项；
polar 配置比较简单，可参考官方文档。angleAxis 与 radiusAxis 配置项略多，但功能上与直角坐标系的 yAxis、xAxis 相似，可对照学习。
基础示例：
实例演示
预览
复制
<!DOCTYPE html>
<html lang="zh-CN">
<head>
<meta charset="utf-8" />
<meta http-equiv="X-UA-Compatible" content="IE=edge" />
<meta name="viewport" content="width=device-width,initial-scale=1.0" />
<title>Echarts Example</title>
</head>
<body>
<div id="main" style="width: 600px;height: 400px"></div>
<!-- 注意引入的echarts文件中需要包含极坐标组件定义 -->
<script src="//cdn.bootcss.com/echarts/4.5.0/echarts.js"></script>
<script type="text/javascript">
var myChart = echarts.init(document.getElementById('main'));
var option = {
toolbox: {
feature: {
saveAsImage: {},
},
},
polar: {},
angleAxis: {
type: 'value',
startAngle: 0,
min: 0,
max: 360,
},
radiusAxis: {
max: 5,
},
series: [
{
// 指定改序列会被应用在极坐标系上
coordinateSystem: 'polar',
type: 'line',
data: [
[4, -155],
[4, -25],
[4, 135],
[4, -90],
[4, 45],
[4, -155],
],
},
],
};
myChart.setOption(option);
</script>
</body>
</html>
运行案例 点击 "运行案例" 可查看在线运行效果
示例效果：
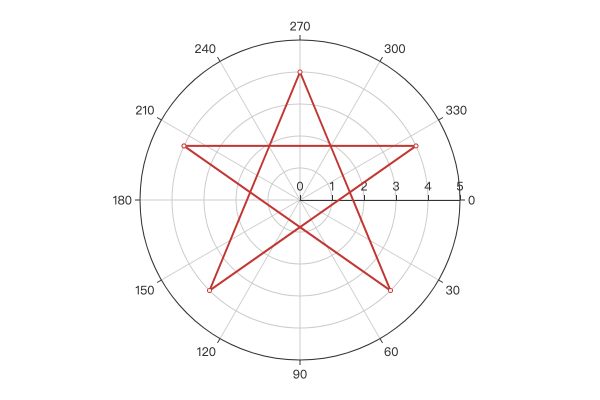
2.2 实现阿基米德螺旋
极坐标通过角度、距离定义坐标位置，所以如果图表的数值关系很容易通过圆角公式计算时，极坐标尤其有用。例如，极坐标下绘制阿基米德螺旋，只需使用公式 r = a + b * θ ：
实例演示
预览
复制
<!DOCTYPE html>
<html lang="zh-CN">
<head>
<meta charset="utf-8" />
<meta http-equiv="X-UA-Compatible" content="IE=edge" />
<meta name="viewport" content="width=device-width,initial-scale=1.0" />
<title>Echarts Example</title>
</head>
<body>
<div id="main" style="width: 600px;height: 400px"></div>
<script src="//cdn.bootcss.com/echarts/4.5.0/echarts.js"></script>
<script type="text/javascript">
var myChart = echarts.init(document.getElementById('main'));
var data = [];
var max = 300;
for (var i = 0; i <= max; i++) {
var angle = Math.ceil(i * ((360 * 6) / max));
// 根据阿基米德螺旋公式：
// r = a + b * θ
var r = angle;
data.push([r, angle]);
}
var option = {
toolbox: {
feature: {
saveAsImage: {},
},
},
polar: {},
angleAxis: {
type: 'value',
startAngle: 0,
min: 0,
max: 360,
},
radiusAxis: {},
series: [{ showSymbol: false, coordinateSystem: 'polar', type: 'line', data: data }],
};
myChart.setOption(option);
</script>
</body>
</html>
运行案例 点击 "运行案例" 可查看在线运行效果
示例效果：
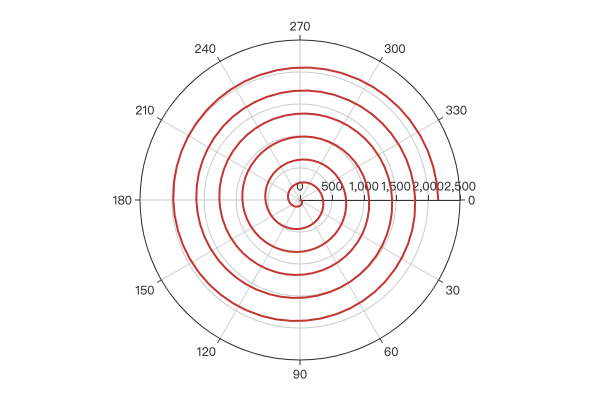
2.3 花瓣图
极坐标下绘制花瓣图，只需实现公式 r = a + b * |sin(c * θ)|：
实例演示
预览
复制
<!DOCTYPE html>
<html lang="zh-CN">
<head>
<meta charset="utf-8" />
<meta http-equiv="X-UA-Compatible" content="IE=edge" />
<meta name="viewport" content="width=device-width,initial-scale=1.0" />
<title>Echarts Example</title>
</head>
<body>
<div id="main" style="width: 600px;height: 400px"></div>
<script src="//cdn.bootcss.com/echarts/4.5.0/echarts.js"></script>
<script type="text/javascript">
var myChart = echarts.init(document.getElementById('main'));
var data = [];
for (var i = 0; i <= 360; i++) {
var x = (i / 360) * Math.PI;
// 花瓣图公式：
// r = a + b * |sin(c * θ)|
var r = 4 + 20 * Math.abs(Math.sin(8 * x));
data.push([r, i]);
}
var option = {
toolbox: {
feature: {
saveAsImage: {},
},
},
polar: {},
angleAxis: { type: 'value', startAngle: 0 },
radiusAxis: { min: 0 },
series: [{ showSymbol: false, coordinateSystem: 'polar', type: 'line', data: data }],
};
myChart.setOption(option);
</script>
</body>
</html>
运行案例 点击 "运行案例" 可查看在线运行效果
示例效果：
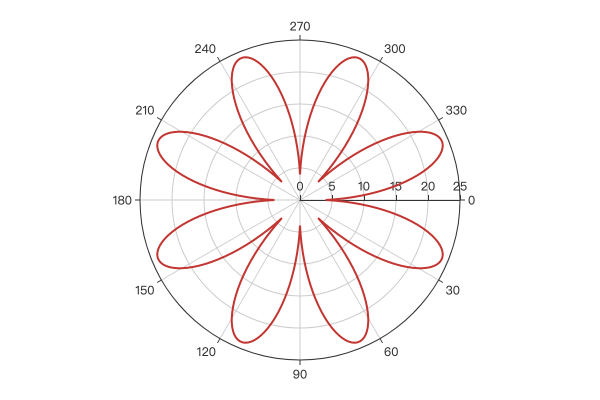
2.4 椭圆
根据椭圆公式可得：
实例演示
预览
复制
<!DOCTYPE html>
<html lang="zh-CN">
<head>
<meta charset="utf-8" />
<meta http-equiv="X-UA-Compatible" content="IE=edge" />
<meta name="viewport" content="width=device-width,initial-scale=1.0" />
<title>Echarts Example</title>
</head>
<body>
<div id="main" style="width: 600px;height: 400px"></div>
<script src="//cdn.bootcss.com/echarts/4.5.0/echarts.js"></script>
<script type="text/javascript">
var myChart = echarts.init(document.getElementById('main'));
var data = [];
var a = 3;
var b = 20;
for (var i = 0; i <= 360; i++) {
var x = (i / 360) * Math.PI;
// 椭圆公式
var r = Math.sqrt(Math.pow(a * b, 2) / (Math.pow(a * Math.sin(x), 2) + Math.pow(b * Math.cos(x), 2)));
data.push([r, i]);
}
var option = {
toolbox: {
feature: {
saveAsImage: {},
},
},
polar: {},
angleAxis: { type: 'value', startAngle: 0 },
radiusAxis: { min: 0 },
series: [{ showSymbol: false, coordinateSystem: 'polar', type: 'line', data: data }],
};
myChart.setOption(option);
</script>
</body>
</html>
运行案例 点击 "运行案例" 可查看在线运行效果
示例效果：
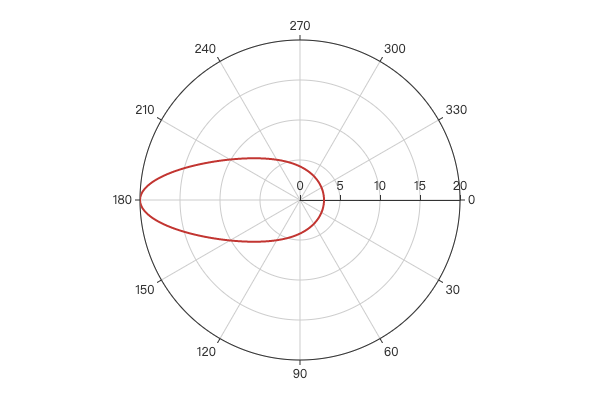
2.5 类别轴
极坐标的 angleAxis、radiusAxis 轴均可设置为类别轴，这一点大大增强了极坐标系的表达能力，与直角坐标系相比，能够再更小的显示面积能展现更多的数据。例如下例：
实例演示
预览
复制
<!DOCTYPE html>
<html lang="zh-CN">
<head>
<meta charset="utf-8" />
<meta http-equiv="X-UA-Compatible" content="IE=edge" />
<meta name="viewport" content="width=device-width,initial-scale=1.0" />
<title>Echarts Example</title>
</head>
<body>
<div id="main" style="width: 600px;height: 400px"></div>
<script src="//cdn.bootcss.com/axios/0.19.2/axios.min.js"></script>
<script src="//cdn.bootcss.com/echarts/4.5.0/echarts.js"></script>
<script type="text/javascript">
async function run() {
// 数据源文件
// 合计62条数据记录
const { data: productions } = await axios.get('./fresh.json');
const myChart = echarts.init(document.getElementById('main'));
const option = {
toolbox: {
feature: {
saveAsImage: {},
},
},
polar: {},
radiusAxis: {
// 设定径向轴为类别类型
type: 'category',
data: productions.map((p) => p.name),
},
angleAxis: { type: 'value' },
series: [
{
coordinateSystem: 'polar',
data: productions.map(({ name, price }) => [name, price]),
type: 'bar',
},
],
label: { show: true },
};
myChart.setOption(option);
}
run();
</script>
</body>
</html>
运行案例 点击 "运行案例" 可查看在线运行效果
示例效果：
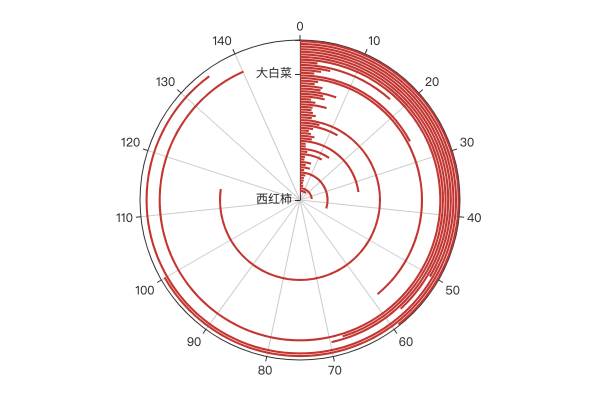
2.6 极坐标下的柱形图
极坐标支持柱形图效果，配置上与折线图相似，多数情况下只需修改折线图的 type 为 bar 即可，示例：
实例演示
预览
复制
<!DOCTYPE html>
<html lang="zh-CN">
<head>
<meta charset="utf-8" />
<meta http-equiv="X-UA-Compatible" content="IE=edge" />
<meta name="viewport" content="width=device-width,initial-scale=1.0" />
<title>Echarts Example</title>
</head>
<body>
<div id="main" style="width: 600px;height: 400px"></div>
<script src="//cdn.bootcss.com/echarts/4.5.0/echarts.js"></script>
<script type="text/javascript">
var myChart = echarts.init(document.getElementById('main'));
var option = {
toolbox: {
feature: {
saveAsImage: {},
},
},
angleAxis: {
type: 'category',
data: ['Mon', 'Tue', 'Wed', 'Thu', 'Fri', 'Sat', 'Sun'],
},
polar: {},
radiusAxis: { type: 'value' },
series: [
{
coordinateSystem: 'polar',
data: [820, 912, 899, 786, 1290, 1330, 1320],
type: 'bar',
name: '水果',
stack: 'search engine',
},
{
coordinateSystem: 'polar',
data: [840, 1002, 789, 934, 1090, 1728, 1468],
type: 'bar',
name: '蔬菜',
stack: 'search engine',
},
{
coordinateSystem: 'polar',
data: [780, 340, 879, 624, 1588, 1624, 1890],
type: 'bar',
name: '百货',
stack: 'search engine',
},
],
label: { show: true },
};
myChart.setOption(option);
</script>
</body>
</html>
运行案例 点击 "运行案例" 可查看在线运行效果
示例效果：
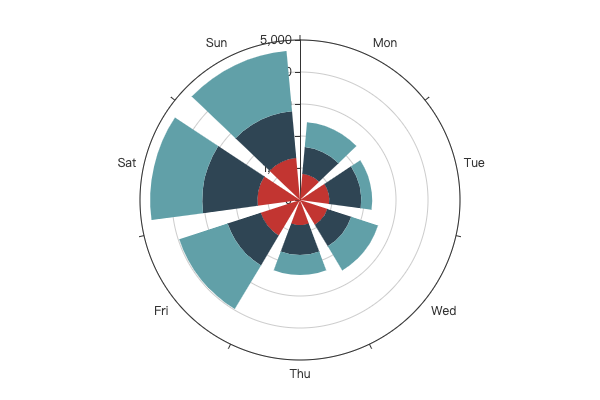
2.7 极坐标下的散点图
极坐标支持散点图图表，配置上与折线图类似，示例：
实例演示
预览
复制
<!DOCTYPE html>
<html lang="zh-CN">
<head>
<meta charset="utf-8" />
<meta http-equiv="X-UA-Compatible" content="IE=edge" />
<meta name="viewport" content="width=device-width,initial-scale=1.0" />
<title>Echarts Example</title>
</head>
<body>
<div id="main" style="width: 600px;height: 400px"></div>
<script src="//cdn.bootcss.com/axios/0.19.2/axios.min.js"></script>
<script src="//cdn.bootcss.com/echarts/4.5.0/echarts.js"></script>
<script type="text/javascript">
function generateData(count) {
const random = (min, max) => Math.round(Math.random() * (max - min) + min);
const cats = ['az', 'bc', 'ed', 'hf', 'ij', 'ek'];
const result = [];
for (let i = 0; i < count; i++) {
const cat = cats[random(0, cats.length - 1)];
result.push([cat, random(0, 10000)]);
}
return { cats, data: result };
}
const { data, cats } = generateData(100);
const myChart = echarts.init(document.getElementById('main'));
const option = {
toolbox: {
feature: {
saveAsImage: {},
},
},
polar: {},
angleAxis: { type: 'value' },
radiusAxis: { type: 'category', data: cats },
series: [
{
coordinateSystem: 'polar',
type: 'scatter',
data,
},
],
};
myChart.setOption(option);
</script>
</body>
</html>
运行案例 点击 "运行案例" 可查看在线运行效果
示例效果：
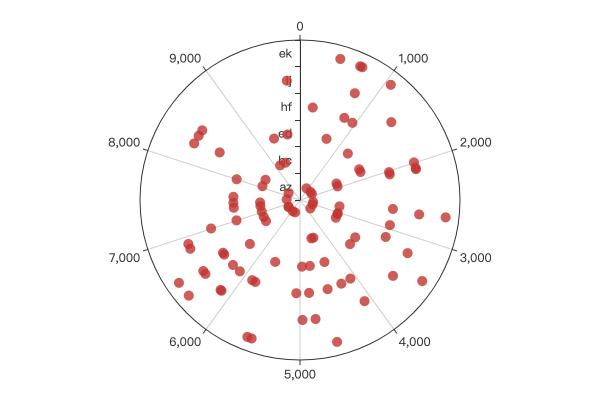
3. 个人经验
极坐标与直角坐标一样，都是为了实现用数学方式表达平面坐标位置，两者通常情况下可以互相转换，不过由于直角坐标系的表达方法更直观，更接近人类直觉，所以直角坐标系的使用会更广泛一些。
4. 小结
本节通过一系列的实例，综合讲述 Echarts 极坐标系各方面的功能特性，包括如何基本配置方法；如何实现阿基米德螺旋、花瓣图、椭圆等特殊图形；以及结合极坐标系实现的柱形图、散点图。
- 还没有人评论，欢迎说说您的想法！
客服
